#music notes | Explore Tumblr Posts and Blogs

canmom · 7 months

Text

Music Theory Notes (for science bitches) 1: chords & such

This is one of these series where I use my blog as a kind of study blog type thing. If you're knowledgeable about music theory, it will be very basic. But that's kind of the problem, I've really struggled to absorb those basics!

When I was a teenager I learned to play violin and played in orchestras. I could read music, and play decently enough, but I didn't really understand music. I just read what was on the page, and played the scales I had to play for exams.

Lately I've been trying to learn music again. This time my instruments are zhonghu, voice, and DAWs. At some point I might get my violin back too. But really, I'm a total beginner again, and this time I want to do it properly.

For a long time when I tried to learn about music I would get overwhelmed with terminology and jargon and conventions. I might watch videos on composition and they'd be interesting but a lot of it would just fly over my head, I'd just have to nod along because I had no idea what all the different types of chord and such were. I tried to learn from sites like musictheory.net, but I found it hard to figure out the logical structure to fit it all into.

I feel like I'm finally making a bit of headway, so it's time to take some notes. The idea here is not just to answer the what, but also to give some sense of why, a motivation. So in a sense this is a first attempt at writing the introduction to music theory I wish I'd had. This is going to assume you know a little bit about physics, but basically nothing about music.

What is music? From first principles.

This is impossible to answer in full generality, especially since as certain people would be quick to remind me, there's a whole corner of avant-garde composers who will cook up counterexamples to whatever claim you make. So let's narrow our focus: I'm talking about the 'most common' type of music in the society I inhabit, which is called 'tonal music'. (However some observations may be relevant to other types of music such as noise or purely rhythmic music.)

Music is generally an art form involving arranging sound waves in time into patterns (in the sense that illustration is about creating patterns on a 2D surface with light, animation is arranging illustrations in time, etc.).

Physically, sound is a pressure wave propagating through a medium, primarily air. As sound waves propagate, they will reflect off surfaces and go into superposition, and depending on the materials around, certain frequencies might be attenuated or amplified. So the way sound waves propagate in a space is very complicated!

But in general we've found we can pretty decently approximate the experience of listening to something using one or two 'audio tracks', which are played back at just one or two points. So for the sake of making headway, we will make an approximation: rather than worry about the entire sound field, we're going to talk about a one-dimensional function of time, namely the pressure at the idealised audio source. This is what gets displayed inside an audio editor. For example, here's me playing the zhonghu, recorded on a mic, as seen inside Audacity.

A wrinkle that is not relevant for this discussion: The idealised 'pressure wave' is a continuous real function of the reals (time to pressure). By contrast, computer audio is quantised in both the pressure level and time, and this is used to reconstruct a continuous pressure wave by convolution at playback time. (Just like a pixel is not a little square, an audio sample is not a constant pressure!) But I'm going to talk about real numbers until quantisation becomes relevant.

When the human eye receives light, the cone cells in the eye respond to the frequencies of EM radiation, creating just three different neural signals, but with incredibly high sensitivity to direction. By contrast, when the human ear receives sound, it is directed into an organ called the cochlea which is kind of like a cone rolled up into a spiral...

Inside this organ, the sound wave moves around the spiral, which has a fascinatingly complex structure that means different frequencies of wave will excite tiny hairs at different points along the tube. In effect, the cochlea performs a short-time Fourier transform of the incoming sound wave. Information about the direction of the incoming wave is given by the way it reflects off the shape of the ear, the difference between ears, and the movement of our head.

So! In contrast to light, where the brain receives a huge amount of information about directions of incoming light but only limited information of the frequency spectrum, with sound we receive a huge amount of information about the frequency spectrum but only quite limited information about its direction.

Music thus generally involves creating patterns with vibration frequencies in the sound wave. More than this, it's also generally about creating repeating patterns on a longer timescale, which is known as rhythm. This has something to do with the way neurons respond to signals but that's something I'm not well-versed in, and in any case it is heavily culturally mediated.

All right, so, this is the medium we have to play with. When we analyse an audio signal that represents music, we chop it up into small windows, and use a Fourier transform to find out the 'frequencies that are present in the signal'.

Most musical instruments are designed to make sounds that are combinations of certain frequencies at integer ratios. For example here is a plot of the [discrete] Fourier transform of a note played on the zhonghu:

The intensity of the signal is written in decibels, so it's actually a logarithmic scale despite looking linear. The frequency of the wave is written in Hertz, and plotted logarithmically as well. A pure sine wave would look like a thin vertical line; a slightly wider spike means it's a combination of a bunch of sine waves of very close frequencies.

The signal consists of one strong peak at 397Hz and nearby frequencies, and a series of peaks at (roughly) integer multiples of this frequency. In this case the second and third peaks are measured at 786Hz, and 1176Hz. Exact integer ratios would give us 794Hz and 1191Hz, but because the first peak is quite wide we'd expect there to be some error.

Some terminology: The first peak is called the fundamental, and the remaining peaks are known as overtones. The frequency of the fundamental is what defines this signal as a particular musical note, and the intensities of the overtone and widths of the peaks define the quality of the note - the thing that makes a flute and a violin playing the same fundamental frequency sound different when we listen to them. If you played two different notes at the same time, you'd get the spectrums of both notes added together - each note has its own fundamental and overtones.

OK, so far that's just basic audio analysis, nothing is specific to music. To go further we need to start imposing some kind of logical structure on the sound, defining relationships between the different notes.

The twelve-tone music system

There are many ways to do this, but in the West, one specific system has evolved as a kind of 'common language' that the vast majority of music is written in. As a language, it gives names to the notes, and defines a space of emotional connotations. We unconsciously learn this language as we go through the process of socialisation, just as we learn to interpret pictures, watch films, etc.

The system I'm about to outline is known as 12-tone equal temperament or "12TET". It was first cooked up in the 16th century almost simultaneously in China and Europe, but it truly became the standard tuning in the West around the 18th century, distilled from a hodgepodge of musical systems in use previously. In the 20th century, classical composers became rather bored of it and started experimenting with other systems of tonality. Nevertheless, it's the system used for the vast majority of popular music, film and game soundtracks, etc.

Other systems exist, just as complex. Western music tends to create scales of seven notes in an octave, but there are variants that use other amounts, like 6. And for example classical Indian music uses its own variant of a seven-note scale; there are also nuances within Western music such as 'just intonation' which we'll discuss in a bit; really, everything in music is really fucking complicated!

I'll be primarily discussing 12TET because 1. it's hard enough to understand just one system and this one is the most accessible; 2. this has a very nice mathematical structure which tickles my autismbrain. However, along the way we'll visit some variants, such as 'Pythagorean intervals'.

The goal is to try and not just say 'this is what the notation means' but explain why we might construct music this way. Since a lot of musical stuff is kept around for historical reasons, that will require some detours into history.

Octaves

So, what's the big idea here? Well, let's start with the idea of an octave. If you have two notes, let's call then M and N, and the frequency of N is twice the frequency of M... well, to the human ear, they sound very very closely related. In fact N is the first overtone of M - if you play M on almost any instrument, you're also hearing N.

Harmony, which we'll talk about in a minute, is the idea that two notes sound especially pleasant together - but this goes even further. So in many many music systems around the world, these two notes with frequency ratio of 2 are actually identified - they are in some sense 'the same note', and they're given the same name. This also means that further powers of 2, of e.g. 4, 8, 16, and so on, are also 'the same note'. We call the relationship between M and N an octave - we say if two notes are 'an octave apart', one has twice the frequency of the other.

For example, a note whose fundamental frequency is 261.626Hz is known as 'C' in the convention of 'concert pitch'. This implies an infinite series of other Cs, but since the human ear has a limited range of frequencies, in practice you have Cs from 8.176Hz up through 16744.036. These are given a series of numbers by convention, so 261.626Hz is called C4, often 'middle C'. 523.251Hz is C5, 1046.502Hz is C6, and so on. However, a lot of the time it doesn't matter which C you're talking about, so you just say 'C'.

But the identification of "C" with 261.626Hz * 2^N is just a convention (known as 'concert pitch'). Nothing is stopping you tuning to any other frequency: to build up the rest of the structure you just need some note to start with, and the rest unfolds using ratios.

Harmony and intervals

Music is less about individual notes, and more about the relationship between notes - either notes played at the same time, or in succession.

Between any two notes we have something called an interval determined by the ratio of their fundamental frequencies. We've already seen one interval: the octave, which has ratio 2.

The next interval to bring up is the 'fifth'. There are a few different variants of this idea, but generally speaking if two notes have a ratio of 1.5, they sound really really nice together. Why is this called a 'fifth'? Historical reasons, there is no way to shake this terminology, we're stuck with it. Just bear with me here, it will become semi-clear in a minute.

In the same vein, other ratios of small integers tend to sound 'harmonious'. They're satisfying to hear together. Ratios of larger integers, by contrast, feel unsatisfying. But this creates an idea of 'tension' and 'resolution'. If you play two notes together that don't harmonise as nicely, you create a feeling of expectation and tension; when you you play some notes that harmonise really well, that 'resolves' the tension and creates a sense of relief.

Building a scale - just intonation

The exact 3:2 integer ratio used in two tuning systems called 'Pythagorean tuning' and 'just intonation'. Using these kinds of integer ratios, you can unfold out a whole series of other notes, and that's how the Europeans generally did things before 12TET came along. For example, in 'just intonation', you might start with some frequency, and then procede in the ratios 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, and at last 2 (the octave). These would be given a series of letters, creating a 'scale'.

What is a scale? A scale is something like the 'colour palette' for a piece of music. It's a set of notes you use. You might use notes from outside the scale but only very occasionally. Different scales are associated with different feelings - for example, the 'major scale' generally feels happy and triumphant, while a 'minor scale' tends to feel sad and forlorn. We'll talk a lot more about scales soon.

In the European musical tradition, a 'scale' consists of seven notes in each octave, so the notes are named by the first seven notes of the alphabet, i.e. A B C D E F G. A scale has a 'base note', and then you'd unfold the other frequencies using the ratios. An instrument such as a piano would be tuned to play a particular scale. The ratios above are one definition of a 'major scale', and starting with C as the base note, the resulting set of notes is called 'C Major'.

All these nice small-number ratios tend to sound really good together. But it becomes rather tricky if you want to play multiple scales on the same instrument. For example, say your piano is tuned in just intonation to C Major. This means, assuming you have a starting frequency we'll call C, you have the following notes available in a given octave:

C, D=(9/8)C, E=(5/4)C, F=(4/3)C, G=(3/2)C [the fifth!], A=(5/3)C, B=(15/8)C, and 2C [the start of the next octave].

Note: the interval we named the 'fifth' is the fifth note in this scale. It's actually the fifth note in the various minor scales too.

But now suppose you want to play with some different notes - let's say a scale we'll call 'A major', which has the same frequency ratios starting on the note we previously called A. Does our piano have the right keys to play this scale?

Well, the next note up from A would be (9/8)A, which would be (9/8)(5/3)C=(15/8)C - that's our B key, so far so good. Then (5/4)A=(5/4)(5/3)C=(25/12)C and... uh oh! We don't have a (25/12)C key, we have 2C, so if we start at A and go up two keys, we have a note that is slightly lower frequency than the one we're looking for.

What this means is that, depending on your tuning, you could only approximate the pretty integer ratios for any scale besides C major. (25/12) is pretty close to 2, so that might not seem so bad, but sometimes we'd land right in between two notes. We can approximate these notes by adding some more 'in between' piano keys. How should we work out what 'extra' keys to include? Well, there were multiple conventions, but we'll see there is some logic to it...

[You might ask, why are you spending so long on this historical system that is now considered obsolete? Well, intervals and their harmonious qualities are still really important in modern music, and it makes most sense to introduce them with the idea of 'small-integer ratios'.]

The semitone

We've seen if we build the 'major scale' using a bunch of 'nice' ratios, we have trouble playing other scales. The gap above may look rather haphazard and arbitrary, but hold on, we're working in exponential space here - shouldn't we be using a logarithmic scale? If I switch to a logarithmic x-axis, we suddenly get a rather appealing pattern...

All the gaps between successive notes are about the same size, except for the gap between E and F, and B and C, which are about half that size. If you try to work that out exactly, you run into the problems we saw above, where C to D is 9/8 or 1.125, but D to E is 10/9 or 1.11111... Even so, you can imagine how people who were playing around with sounds might notice, damn, these are nice even steps we have here. Though you might also notice places where, in this scheme, it's not completely even - for example G to A (ratio 10/9) is noticeably smaller than A to B (ratio 9/8).

We've obliquely approached the idea of dividing the octave up into 12 steps, where each step is about the size of the gap between E and F or B and C. We call each of these steps a 'semitone'. Two semitones make a 'whole tone'. We might fill in all the missing semitones in our scale here using whole-number ratios, which gives you the black keys on the piano. There are multiple schemes for doing this, and the ratios tend to get a bit uglier. In the system we've outlined so far, a 'semitone' is not a fixed ratio, even though it's always somewhere around 1.06.

The set of 12 semitones is called the 'chromatic scale'. It is something like the 'colour space' for Western music. When you compose a piece, you select some subset of the 12 semitones as your 'palette' - the 'scale of' a piece of music.

But we still have a problem here, which is the unevenness of the gaps we discussed above. This could be considered a feature, not a bug, since each scale would have its own 'character' - it's defined by a slightly different set of ratios. But it does add a lot of complication when moving between scales.

So let's say we take all this irregularity as a bug, and try to fix it. The solution is 'equal temperament', which is the idea that the semitone should always be the exact same ratio, allowing the instrument to play any scale you please without difficulty.

Posed like this, it's easy to work out what that ratio should be: if you want 12 equal steps to be an octave, each step must be the 12th root of 2. Which is an irrational number that is about 1.05946...

At this point you say, wait, Bryn, didn't you just start this all off by saying that the human ear likes to hear nice simple integer ratios of frequencies? And now you're telling me that we should actually use an irrational number, which can't be represented by any integer ratio? What gives? But it turns out the human ear isn't quite that picky. If you have a ratio of 7 semitones, or a ratio of 2^(7/12)=1.4983..., that's close enough to 1.5 to feel almost as good. And this brings a lot of huge advantages: you can easily move ('transpose') between different scales of the same type, and trust that all the relevant ratios will be the same.

Equal temperament was the eventual standard, but there was a gradual process of approaching it called stuff like 'well-tempered' or 'good temperament'. One of the major steps along the way was Bach's collection 'the well-tempered klavier', showing how a keyboard instrument with a suitable tuning could play music in every single established scale. Here's one of those pieces:

youtube

Although we're using these irrational numbers, inside the scale are certain intervals that are considered to have certain meanings - some that are 'consonant' and some that are 'dissonant'. We've already mentioned the 'fifth', which is the 'most consonant' ratio. The fifth consists of 7 semitones and it's roughly a 1.5 ratio in equal temperament. Its close cousin is the 'fourth', which consists of 5 semitones. Because it's so nice, the fifth is kind of 'neutral' - it's just there but it doesn't mean a lot on its own.

For the other important intervals we've got to introduce different types of scale.

The scale zoo

So, up above we introduced the 'major' scale. In semitones, the major scale is intervals of 2, 2, 1, 2, 2, 2, 1. This is also called a 'mode', specifically the 'Ionian mode'. There are seven different 'modes', representing different permutations of these intervals, which all have funky Greek names.

The major scale generally connotes "upbeat, happy, triumphant". There are 12 different major scales, taking the 12 different notes of the chromatic scale as the starting point for each one.

Next is the minor scale, which tends to feel more sad or mysterious. Actually there are a few different minor scales. The 'natural minor' goes 2, 1, 2, 2, 1, 2, 2. You might notice this is a cyclic permutation of the major scale! So in fact a natural minor scale is the same set of notes as a major scale. What makes it different?

Well, remember when we talked about tension and resolution? It's about how the notes are organised. Our starting note is the 'root' note of the scale, usually established early on in the piece of music - quite often the very first note of the piece. The way you move around that root note determines whether the piece 'feels' major or minor. So every major scale has a companion natural minor scale, and vice versa. The set of notes in a piece is enough to narrow it down to one minor and one major, but you have to look closer to figure out which one is most relevant.

The 'harmonic minor' is almost the same, but it raises the second-last note (the 7th) a semitone. So its semitone intervals are 2, 1, 2, 2, 1, 3, 1.

The 'melodic minor' raises both the 6th and 7th by one semitone, (edit: but usually only on the way up). So its semitone intervals are 2, 1, 2, 2, 2, 2, 1. (edit: When you come back down you tend to use the natural minor.)

If you talk about a 'minor scale' unqualified, you mean the natural minor. It's also the 'Aeolian mode' in that system of funky Greek names I mentioned earlier.

So that leads to a set of 24 scales, a major and minor scale for every semitone. These are the most common scale types that almost all Western tonal music is written in.

But we ain't done. Because remember I said there were all those other "modes"? These are actually just cyclic permutations of the major scale. There's a really nerdy Youtube channel called '8-bit music theory' that has a bunch of videos analysing them in the context of videogame music which I'm going to watch at some point now I finally have enough background to understand wtf he's talking about.

youtube

And of top of that you have all sorts of other variants that come from shifting a note up or down a semitone.

The cast of intervals

OK, so we've established the idea of scales. Now let's talk intervals. As you might guess from the 'fifth', the intervals are named after their position in the scale.

Let me repeat the two most common scale modes, in terms of number of semitones relative to the root note:

position: 1, 2, 3, 4, 5, 6, 7, 8 major: 0, 2, 4, 5, 7, 9, 11, 12 minor: 0, 2, 3, 5, 7, 8, 10, 12

So you can see the fourth and fifth are the same in both. But there's a difference in three places: the third, the sixth, and the seventh. In each case, the minor is down a semitone from the major.

The interval names are... not quite as simple as 'place in the scale', but that's mostly how it works. e.g. the 'major third' is four semitones and the 'minor third' is three.

The fourth and fifth, which are dual to each other (meaning going up a fifth takes you to the same note as going down a fourth, and vice versa) are called 'perfect'. The note right in between them, an interval of 6 semitones, is called the 'tritone'.

(You can also refer to these intervals as 'augmented' or 'diminished' versions of adjacent intervals. Just in case there wasn't enough terminology in the air. See the table for the names of every interval.)

So, with these names, what's the significance of each one? The thirds, sixths and sevenths are important, because they tell us whether we're in minor or major land when we're building chords. (More on that soon.)

The fifth and the octave are super consonant, as we've said. But the notes that are close to them, like the seventh, the second and even more so the tritone, are quite dissonant - they're near to a nice thing and ironically that leads to awkward ratios which feel uncomfy to our ears. So generally speaking, you use them to build tension and anticipation and set up for a resolution later. (Or don't, and deliberately leave them hanging.)

Of course all of these positions in the scale also have funky Latin names that describe their function.

There's a lot more complicated nuances that make the meaning of a particular interval very contextual, and I certainly couldn't claim to really understand in much depth, but that's basically what I understand about intervals so far.

Our goofy-ass musical notation system

So if semitones are the building block of everything, naturally the musical notation system we use in the modern 12TET era spaces everything out neatly in terms of semitones, right?

Right...?

Lmao no. Actually sheet music is written so that each row of the stave (or staff, the five lines you write notes on) represents a note of the C major scale. All the notes that aren't on the C major scale are represented with special symbols, namely ♯ (read 'sharp') which means 'go up a semitone', and ♭ (read 'flat') which means 'go down a semitone'. That means the same note can be notated in two different ways: A♯ and B♭ are the same note.

The above image shows the chromatic scale, notated in two different ways. Every step is exactly one semitone.

Since a given scale might end up using one of these 'in between' notes that has to be marked sharp or flat, and you don't want to do that for every single time that note appears. Luckily, it turns out that each major/minor scale pair ends up defining a unique set of notes to be adjusted up or down a semitone, called the 'key signature'. So you can write the key signature at the beginning of the piece, and it lasts until you change key signature. For example, the key of 'A♭ major' ends up having four sharps:

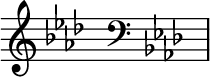
There is a formula you can use to work out the set of sharps or flats to write for a given key. (That's about the point I checked out on musictheory.net.)

There is some advantage to this system, which is that it very clearly tells you when the composer intends to shift into a different scale, and it saves space since with the usual scales there are no wasted lines. But it's also annoyingly arbitrary. You just have to remember that B to C is only a semitone, and the same for E to F.

What are those weird squiggly symbols? Those are 'clefs'. Each one assigns notes to specific lines. The first one 𝄞 is the 'treble clef', the second one 𝄢 is the 'bass clef'. Well, actually these are the 'G-clef' and the 'F-clef', and where they go on the stave determines note assignment, but thankfully this has been standardised and you will only ever see them in one place. The treble clef declares the lines to be E G B D F and the bass clef G B D F A.

There is also a rarer 'C-clef' which looks like 𝄡. This is usually used as the 'Alto clef' which means F A C E G.

This notation system seems needlessly convoluted, but we're rather stuck with it, because most of the music has been written in it already. It's not uncommon for people to come up with alternative notations, though, such as 'tabs' for a stringed instrument which indicate which position should be played on each string. Nowadays on computers, a lot of DAWs will instead use a 'piano roll' presentation which is organised by semitone.

And then there's chords.

Chords! And arpeggios!

A chord is when you play 3 or more notes at the same time.

Simple enough right? But if you wanna talk about it, you gotta have a way to give them names. And that's where things get fucking nuts.

But the basic chord type is a 'triad', consisting of three notes, separated by certain intervals. There are two standard types, which you basically assemble by taking every other note of a scale. In terms of semitones, these are:

Major triad: 0 - 4 - 7 Minor triad: 0 - 3 - 7

Then there's a bunch of variations, for example:

Augmented: 0 - 4 - 8 Diminished: 0 - 3 - 6 Suspended: 0 - 2 - 7 (sus2) or 0 - 5 - 7 (sus4) Dominant seventh: 0 - 4 - 7 - 10 Power: 0 - 7

There is a notation scheme for chords in pop, jazz, rock, etc., which starts with a root note and then adds a bunch of superscripts to tell you about any special features of a chord. So 'C' means the C Major triad (namely C,E,G) and 'Cm' or 'c' means the C Minor triad (namely C,E♭,G).

In musical composition, you usually tend to surround the melody (single voice) with a 'chord progression' that both harmonises and creates a sense of 'movement' from one chord to another. Some instruments like guitar and piano are really good at playing chords. On instruments that can't play chords, they can still play 'arpeggios', which is what happens if you take a chord and unroll it into a sequence of notes. Or you play in an ensemble and harmonise with the other players to create a chord together. Awww.

Given a scale, you can construct a series of seven triad chords, starting from each note of the scale. These are generally given scale-specific Roman numerals corresponding to the position in the scale, and they're used to analyse the progression of chords in a song. I pretty much learned about this today while writing this post, so I can't tell you much more than that.

Right now, that's about as far as I've gotten with chords. On a violin, you can play just two strings at the same time after all - I never had much need to learn about them so it remains a huge hole in my understanding of music. I can't recognise chords by ear at all. So I gotta learn more about them.

As much as I wrote this for my own benefit... if you found this post interesting, let me know. I might write more if people find this style of presentation appealing. ^^'

#Youtube #music #music theory #notes #music notes

239 notes · View notes

canmom · 4 months

Text

Music Theory notes (for science bitches) part 3: what if. there were more notes. what if they were friends.

Hello again, welcome back to this series where I try and teach myself music from first principles! I've been making lots of progress on zhonghu in the meantime, but a lot of it is mechanical/technical stuff about like... how you hold the instrument, recognising pitches

In the first part I broke down the basic ideas of tonal music and ways you might go about tuning it in the 12-tone system, particularly its 'equal temperament' variant [12TET]. The second part was a brief survey of the scales and tuning systems used in a selection of music systems around the world, from klezmer to gamelan - many of them compatible with 12TET, but not all.

So, as we said in the first article, a scale might be your 'palette' - the set of notes you use to build music. But a palette is not a picture. And hell, in painting, colour implies structure: relationships of value, saturation, hue, texture and so on which create contrast and therefore meaning.

So let's start trying to understand how notes can sit side by side and create meaning - sequentially in time, or simultaneously as chords! But there are still many foundations to lay. Still, I have a go at composing something at the end of this post! Something very basic, but something.

Anatomy of a chord

I discussed this very briefly in the first post, but a chord is when you play two or more notes at the same time. A lot of types of tonal musical will create a progression of chords over the course of a song, either on a single instrument or by harmonising multiple instruments in an ensemble. Since any or all of the individual notes in a chord can change, there's an enormous variety of possible ways to go from one chord to another.

But we're getting ahead of ourselves. First of all I wanna take a look at what a chord actually is. Look, pretty picture! Read on to see what it means ;)

So here is a C Minor chord, consisting of C, D# and G, played by a simulated string quartet:

(In this post there's gonna be sound clips. These are generated using Ableton, but nothing I talk about should be specific to any one DAW [Digital Audio Workstation]. Ardour appears to be the most popular open source DAW, though I've not used it. Audacity is an excellent open source audio editor.)

Above, I've plotted the frequency spectrum of this chord (the Fourier transform) calculated by Audacity. The volume is in decibels, which is a logarithmic scale of energy in a wave. So this is essentially a linear-log plot.

OK, hard to tell what's going on in there right? The left three tall spikes are the fundamental frequencies of C4 (262Hz), D♯4 (310Hz), and G4 (393Hz). Then, we have a series of overtones of each note, layered on top of each other. It's obviously hard to tell which overtone 'belongs to' which note. Some of the voices may in fact share overtones! But we can look at the spectra of the indivudal notes to compare. Here's the C4 on its own. (Oddly, Ableton considered this a C3, not a C4. as far as I can tell the usual convention is that C4 is 261.626Hz, so I think C4 is 'correct'.)

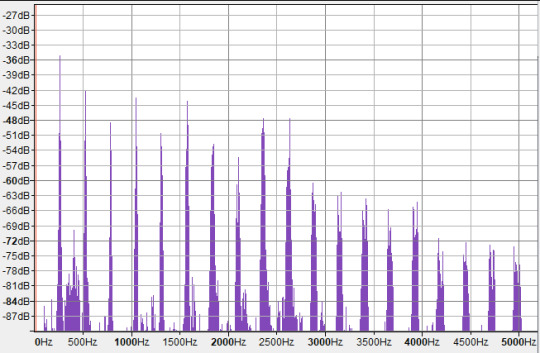
Here, the strongest peaks are all at integer multiples of the fundamental frequency, so they look evenly spaced in linear frequency-space. These are not all C. The first overtone is an octave above (C5), then we have three times the frequency of C4 - which means it's 1.5 times the frequency of C5, i.e. a perfect fifth above it! This makes it a G. So our first two overtones are in fact the octave and the fifth (plus an octave). Then we get another C (C6), then in the next octave we have frequencies pretty close to E6, G6 and A♯6 - respectively, intervals of a major third, a perfect fifth, and minor 7th relative to the root (modulo octaves).

However, there are also some weaker peaks. Notably, in between the first and second octave is a cluster of peaks around 397-404Hz, which is close to G4 - another perfect fifth! However, it's much much weaker than the overtones we discussed previously.

The extra frequencies and phase relationships give the timbre of the note, its particular sound - in this case you could say the sense of 'softness' in the sound compared to, for example, a sine wave, or a perfect triangle wave which would also have harmonics at all integer frequencies.

Perhaps in seeing all these overtones, we can get an intuitive impression of why chords sound 'consonant'. If the frequencies of a given note are already present in the overtones, they will reinforce each other, and (in extremely vague and unscientific terms) the brain gets really tickled by things happening in sync. However, it's not nearly that simple. Even in this case, we can see that frequencies do not have to be present in the overtone spectrum to create a pleasing sense of consonance.

Incidentally, this may help explain why we consider two notes whose frequencies differ by a factor of 2 to be 'equivalent'. The lower note contains all of the frequencies of the higher note as overtones, plus a bunch of extra 'inbetween' frequencies. e.g. if I have a note with fundamental frequency f, and a note with frequency 2f, then f's overtones are 2f, 3f, 4f, 5f, 6f... while 2f's overtones are 2f, 4f, 6f, 8f. There's so much overlap! So if I play a C, you're also hearing a little bit of the next C up from that, the G above that, the C above that and so on.

For comparison, if we have a note with frequency 3f, i.e. going up by a perfect fifth from the second note, the frequencies we get are 3f, 6f, 9f, 12f. Still fully contained in the overtones of the first note, but not quite as many hits.

Of course, the difference between each of these spectra is the amplitudes. The spectrum of the lower octave may contain the frequencies of the higher octave, but much quieter than when we play that note, and falling off in a different way.

(Note that a difference of ten decibels is very large: it's a logarithmic scale, so 10 decibels means 10 times the energy. A straight line in this linear-log plot indicates a power-law relationship between frequency and energy, similar to the inverse-square relationship of a triangle wave, where the first overtone has a quarter of the power, the second has a ninth of the power, and so on.)

So, here is the frequency spectrum of the single C note overlaid onto the spectrum of the C minor chord:

Some of the overtones of C line up with the overtones of the other notes (the D# and G), but a great many do not. Each note is contributing a bunch of new overtones to the pile. Still, because all these frequencies relate back to the base note, they feel 'related' - we are drawn to interpret the sounds together as a group rather than individually.

Our ears and aural system respond to these frequencies at a speed faster than thought. With a little effort, you can pick out individual voices in a layered composition - but we don't usually pick up on individual overtones, rather the texture created by all of them together.

I'm not gonna take the Fourier analysis much further, but I wanted to have a look at what happens when you crack open a chord and poke around inside.

However...

In Western music theory terms, we don't really think about all these different frequency spikes, just the fundamental notes. (The rest provides timbre). We give chords names based on the notes of the voices that comprise them. Chord notation can get... quite complicated; there are also multiple ways to write a given chord, so you have a degree of choice, especially once you factor in octave equivalence! Here's a rapid-fire video breakdown:

youtube

Because you have all these different notes interacting with each other, you further get multiple interactions of consonance and dissonance happening simultaneously. This means there's a huge amount of nuance. To repeat my rough working model, we can speak of chords being 'stable' (meaning they contain mostly 'consonant' relations like fifths and thirds) or 'unstable' (featuring 'dissonant' relations like semitones or tritones), with the latter setting up 'tension' and the former resolving it.

However, that's so far from being useful. To get a bit closer to composing music, it would likely help to go a bit deeper, build up more foundations and so on.

In this post and subsequent ones, I'm going to be taking things a little slower, trying to understand a bit more explicitly how chords are deployed.

An apology to Western music notation

In my first post in this series, I was a bit dismissive of 'goofy' Western music notation. What I was missing is that the purpose of Western music notation is not to clearly show the mathematical relationships between notes (something that's useful for learning!)... but to act as a reference to use while performing music. So it's optimising for two things: compactness, and legibility of musical constructs like phrasing. Pedagogy is secondary.

Youtuber Tantacrul, lead developer of the MuseScore software, recently made a video running over a brief history of music notation and various proposed alternative notation schemes - some reasonable, others very goofy. Having seen his arguments, he makes a pretty good case for why the current notation system is actually a reasonable compromise... for representing tonal music on the 12TET system, which is what it's designed for.

So with that in mind, let me try and give a better explanation of the why of Western music notation.

In contrast to 'piano roll' style notation where you represent every possible note in an absolute way, here each line of the stave (staff if you're American) represents a scale degree of a diatonic scale. The key signature locates you in a particular scale, and all the notes that aren't on that scale are omitted for compactness (since space is at an absolute premium when you have to turn pages during a performance!). If you're doing something funky and including a note outside the scale, well that's a special case and you give it a special-case symbol.

It's a similar principle to file compression: if things are as-expected, you omit them. If things are surprising, you have to put something there.

However, unlike the 简谱 jiǎnpǔ system which I've been learning in my erhu lessons, it's not a free-floating system which can attach to any scale. Instead, with a given clef, each line and space of the stave has one of three possible notes it could represent. This works, because - as we'll discuss momentarily - the diatonic scales can all be related to each other by shifting certain scale degrees up or down in semitones. So by indicating which scale degrees need to be shifted, you can lock in to any diatonic scale. Naisuu.

This approach, which lightly links positions to specific notes, keeps things reasonably simple for performers to remember. In theory, the system of key signatures helps keep things organised, without requiring significant thought while performing.

That is why have to arbitrarily pick a certain scale to be the 'default'; in this case, history has chosen C major/A minor. From that point, we can construct the rest of the diatonic scales as key signatures using a cute mathematical construct called the 'circle of fifths'.

How key signatures work (that damn circle)

So, let's say you have a diatonic major scale. In piano roll style notation, this looks like (taking C as our base note)...

And on the big sheet of scales, like this:

Now, let's write another diatonic major scale, a fifth up from the first. This is called transposition. For example, we could transpose from C major to G major.

Thanks to octave equivalency, we can wrap these notes back into the same octave as our original scale. (In other words, we've added 7 semitones to every note in our original scale, and then taken each one modulo 12 semitones.) Here, I duplicate the pattern down an octave.

Now, if we look at what notes we have in both scales, over the range of the original major scale.

Well, they're almost exactly the same... but the fourth note (scale degree) is shifted up by one semitone.

In fact, we've seen this set of notes before - it is after all nothing more than a cyclic permutation of the major scale. We've landed on the 'Lydian mode', one of the seven 'modes' of the diatonic major scale we discussed in previous posts. We've just found out that the Lydian mode has the same notes as a major scale starting a fifth higher. In general, whether we think of it as a 'mode' or as a 'different major scale' is a matter of where we start (the base note). I'm going to have more to say about modes in a little bit.

With this trick in mind, we produce a series of major scales starting a fifth higher each time. It just so happens that, since the fifth is 7 semitones, which is coprime with the 12 semitones of 12TET, this procedure will lead us through every single possible starting note in 12TET (up to octave equivalency).

So, each time we go up a fifth, we add a sharp on the fourth degree of the previous scale. This means that every single major scale in 12TET can be identified by a unique set of sharps. Once you have gone up 12 fifths, you end up with the original set of notes.

This leads us to a cute diagram called the "circle of fifths".

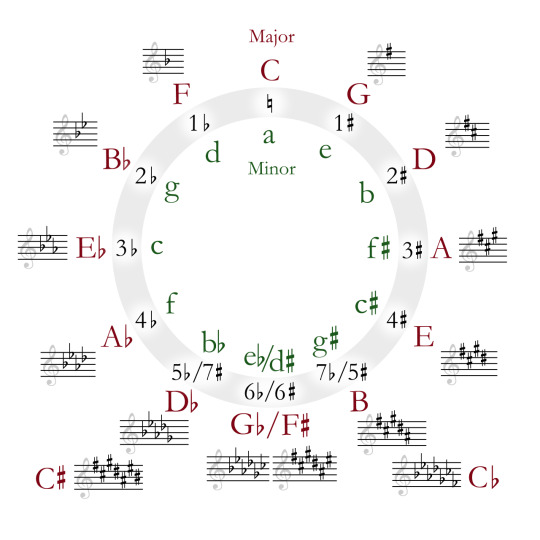
Because going up a fifth is octave-equivalent to going down a fourth, we can also look back one step on the circle to find out which note needs to be made sharper. So, from C major to G major, we have to sharpen F - the previous note on the circle from C. From G major to D major, we have to sharpen C. From D major to A major, we have to sharpen G. And so on.

By convention, when we write a key signature to define the particular scale we're using, we write the sharps out in circle-of-fifths order like this. The point of this is to make it easy to tell at a glance what scale you're in... assuming you know the scales already, anyway. This is another place where the aim of the notation scheme is for a compact representation for performers rather than something that makes the logical structure evident to beginners.

Also by convention, key signatures don't include the other octaves of each note. So if F is sharp in your key signature, then every F is sharp, not just the one we've written on the stave.

This makes it less noisy, but it does mean you don't have a convenient visual reminder that the other Fs are also sharp. We could imagine an alternative approach where we include the sharps for every visible note, e.g. if we duplicate every sharp down an octave for C♯ major...

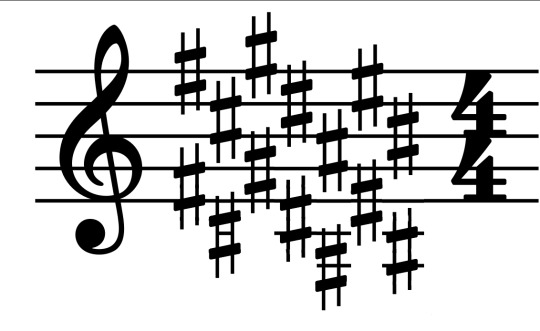
...but maybe it's evident why this would probably be more confusing than helpful!

So, our procedure returns the major scales in order of increasing sharps. Eventually you have added seven sharps, meaning every scale degree of the original starting scale (in this case, C Major) is sharpened.

What would it mean to keep going past this point? Let's hop in after F♯ Major, at the bottom of the Circle of Fifths; next you would go to C♯ Major by sharpening B. So far so good. At this point we have sharps everywhere, so the notes in your scale go... C♯ D♯ E♯ F♯ G♯ A♯ B♯ C♯ ...except that E♯ is the same as F, and B♯ is the same as C, so we could write that as C♯ D♯ F F♯ G♯ A♯ C C♯

But then to get to 'G♯ Major', you would need to sharpen... F♯? That's not on the original C-major scale we started with ! You could say, well, essentially this adds up to two sharps on F, so it's like F♯♯, taking you to G. So now you have...

G♯ A♯ C C♯ D♯ F G G♯

...and the line of the stave that you would normally use for F now represents a G. You could carry on in this way, eventually landing all the way back at the original set of notes in C Major (bold showing the note that just got sharpened in each case):

D♯ F G G♯ A♯ C D D♯ A♯ C D D♯ F G A A♯ F G A A♯ C D E F C D E F G A B C

But that sounds super confusing - how would you even represent the double sharps on the key signature? It would break the convention that each line of the stave can only represent three possible notes. Luckily there's a way out. We can work backwards, going around the circle the other way and flattening notes. This will hit the exact same scales in the opposite order, but we think of their relation to the 'base' scale differently.

So, let's try starting with the major scale and going down a fifth. We could reason about this algebraically to work out that sharpening the fourth while you go up means flattening the seventh when you go down... but I can also just put another animation. I like animations.

So: you flatten the seventh scale degree in order to go down a fifth in major scales. By iterating this process, we can go back around the circle of fifths. For whatever reason, going down this way we use flats instead of sharps in the names of the scale. So instead of A♯ major we call it B♭ major. Same notes in the same order, but we think of it as down a rung from F major.

In terms of modes, this shows that the major scale a fifth down from a given root note has the same set of notes as the "mixolydian mode" on the original root note. ...don't worry, you don't gotta memorise this, there is not a test! Rather, the point of mentioning these modes is to underline that whether you're in a major key, minor key, or one of the various other modes is all relative to the note you start on. We'll see in a moment a way to think about modes other than 'cyclic permutation'.

Let's try the same trick on the minor key.

Looks like this time, to go up we need to sharpen the sixth degree, and to go down we need to flatten the second degree. As algebra demands, this gives us the exact same sequence of sharps and flats as the sequence of major scales we derived above. After all, every major scale has a 'relative minor' which can be achieved by cyclically permuting its notes.

Going up a fifth shares the same notes with the 'Dorian mode' of the original base note, and going down a fifth shares the same notes with the 'Phrygian mode'.

Here's a summary of movement around the circle of fifths. The black background indicates the root note of the new scale.

Another angle on modes

In my first two articles, I discussed the modes of the diatonic scale. Leaping straight for the mathematically simplest definition (hi Kolmogorov), I defined the seven 'church modes' as simply being cyclic permutations of the intervals of the major scale. Which they are... but I'm told that's not really how musicians think of them.

Let's grab the chart of modes again. (Here's the link to the spreadsheet).

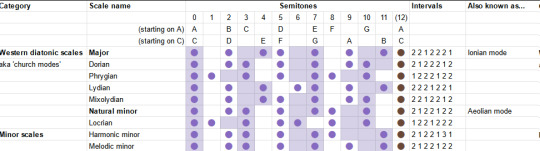
We can get to these modes by cyclically permuting the others, but we can also get to them by making a small adjustment of one to a few particular scale degrees. When you listen to a piece of music, you're not really doing cyclic permutations - you're building up a feeling for the pattern of notes based on your lifelong experience of hearing music that's composed in this system. So the modes will feel something like 'major until, owo what's this, the seventh is not where I thought it would be'.

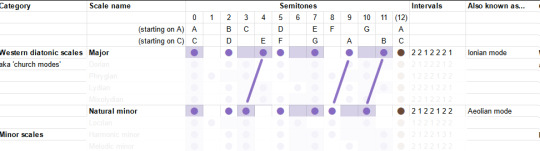
Since the majority of music is composed using major and minor modes, it's useful therefore to look at the 'deltas' relative to these particular modes.

To begin with, what's the difference between major and minor? To go from major to natural minor, you shift the third, sixth and seventh scale degrees down by one semitone.

So those are our two starting points. For the others, I'm going to be consulting the most reliable music theory source (some guy on youtube) to give suggestions of the emotional connotations these can bring. The Greek names are not important, but I am trying to build a toolbox of elements here, so we can try our hand at composition. So!

The "Dorian mode" is like the natural minor, but the sixth is back up a semitone. It's described as a versatile mode which can be mysterious, heroic or playful. I guess that kinda makes sense, it's like in between the major and minor?

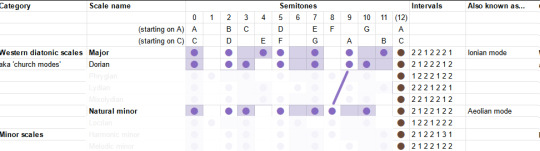
The "Phrygian mode" is natural minor but you also lower the 2nd - basically put everything as low as you can go within the diatonic modes. It is described as bestowing an ominous, threatening feeling.

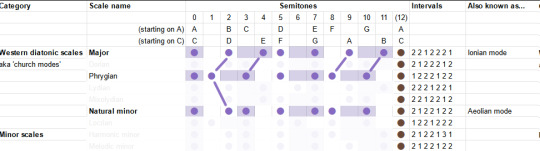
The "Lydian mode" is like the major scale, but you shift the fourth up a semitone, landing on the infamous tritone. It is described as... uh well actually the guy doesn't really give a nice soundbitey description of what this mode sounds like, besides 'the brighest' of the seven, this video's kinda more generally about composition, whatever. But generally it's pretty big and upbeat I think.

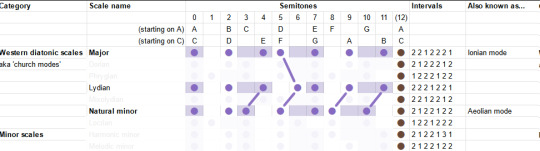
The "Mixolydian" mode is the major, but with the seventh down a semitone. So it's like... a teeny little bit minor. It's described as goofy and lighthearted.

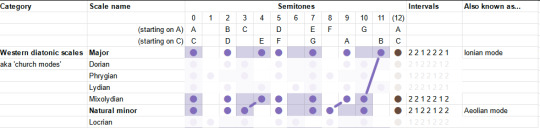
We've already covered the Aeolian/Natural Minor, so that leaves only the "Locrian". This one's kinda the opposite of the Lydian: just about everything in the major scale is flattened a bit. Even from the minor it flattens two things, and gives you lots of dissonance. This one is described as stereotypically spooky, but not necessarily. "One of the least useful", oof.

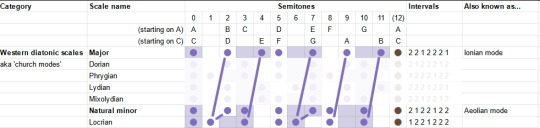
Having run along the catalogue, we may notice something interesting. In each case, we always either only sharpen notes, or only flatten notes relative to the major and minor scales. All those little lines are parallel.

Indeed, it turns out that each scale degree has one of two positions it can occupy. We can sort the diatonic modes according to whether those degrees are in the 'sharp' or 'flat' position.

This is I believe the 'brightness' mentioned above, and I suppose it's sort of like 'majorness'. So perhaps we can think of modes as sliding gradually from the ultra-minor to the infra-major? I need to experiment and find out.

What have we learned...?

Scale degrees are a big deal! The focus of all this has been looking at how different collections of notes relate to each other. We sort our notes into little sets and sequences, and we compare the sets by looking at 'equivalent' positions in some other set.

Which actually leads really naturally into the subject of chord progressions.

So, musical structure. A piece of tonal music as a whole has a "palette" which is the scale - but within that, specific sections of that piece of music will pick a smaller subset of the scale, or something related to the scale, to harmonise.

The way this goes is typically like this: you have some instruments that are playing chords, which gives the overall sort of harmonic 'context', and you have a single-voiced melody or lead line, which stands out from the rest, often with more complex rhythms. This latter part is typically what you would hum or sing if you're asked 'how a song goes'. Within that melody, the notes at any given point are chosen to harmonise with the chords being played at the same time.

The way this is often notated is to write the melody line on the stave, and to write the names of chords above the stave. This may indicate that another hand or another instrument should play those chords - or it may just be an indication for someone analysing the piece which chord is providing the notes for a given section.

So, you typically have a sequence of chords for a piece of music. This is known as a chord progression. There are various analytical tools for cracking open chord progressions, and while I can't hope to carry out a full survey, let me see if I can at least figure out my basic waypoints.

Firstly, there are the chords constructed directly from scales - the 'triad' chords, on top of which can be piled yet more bonus intervals like sevenths and ninths. Starting from a scale, and taking any given scale degree as the root note, you can construct a chord by taking every other subsequent note.

So, the major scale interval pattern goes 2 2 1 2 2 2 1. We can add these up two at a time, starting from each position, to get the chords. For each scale degree we therefore get the following intervals relative to the base note of the chord...

I. 0 4 7 - major

ii. 0 3 7 - minor

iii. 0 3 7 - minor

IV. 0 4 7 - major

V. 0 4 7 - major

vi. 0 3 7 - minor

viiᵒ. 0 3 6 - diminished

Now hold on a minute, where'd those fuckin Roman numerals come from? I mentioned this briefly in the first post, but this is Roman numeral analysis, which is used to talk about chord progressions in a scale-independent way.

Here, a capital Roman numeral represents a major triad; a lowercase Roman numeral represents a minor triad; a superscript 'o' represents a dimished triad (minor but you lower the fifth down to the tritone); a superscript '+' represents an augmented triad (major but you boost the fifth up to the major sixth).

So while regular chord notation starts with the pitch of the base note, the Roman numeral notation starts with a scale degree. This way you can recognise the 'same' chord progression in songs that are in quite different keys.

OK, let's do the same for the minor scale... 2 1 2 2 1 2 2. Again, adding them up two at a time...

i. 0 3 7 - minor

iiᵒ. 0 3 6 - diminished

III. 0 4 7 - major

iv. 0 3 7 - minor

v. 0 3 4 - minor

VI. 0 4 7 - major

VII. 0 4 7 - major

Would you look at that, it's a cyclic permutation of the major scale. Shocker.

So, both scales have three major chords, three minor chords and a diminished chord in them. The significance of each of these positions will have to be left to another day though.

What does it mean to progress?

So, you play a chord, and then you play another chord. One or more of the voices in the chord change. Repeat. That's all a chord progression is.

You can think of a chord progression as three (or more) melodies played as once. Only, there is an ambiguity here.

Let's say, idk, I threw together this series of chords, it ended up sounding like it would be something you'd hear in an old JRPG dungeon, though maybe that's just 'cos it's midi lmao...

I emphasise at this point that I have no idea what I'm doing, I'm just pushing notes around until they sound good to me. Maybe I would know how to make them sound better if I knew more music theory! But also at some point you gotta stop theorising and try writing music.

So this chord progression ended up consisting of...

Csus2 - Bm - D♯m - A♯m - Gm - Am - F♯m - Fm - D - Bm

Or, sorted into alphabetical order, I used...

Am, A♯m, Bm, Csus2, D, D♯m, Fm, F♯m, Gm

Is that too many minor chords? idk! Should all of these technically be counted as part of the 'progression' instead of transitional bits that don't count? I also dk! Maybe I'll find out soon.

I did not even try to stick to a scale on this, and accordingly I'm hitting just about every semitone at some point lmao. Since I end on a B minor chord, we might guess that the key ought to be B minor? In that case, we can consult the circle of fifths and determine that F and C would be sharp. This gives the following chords:

Bm, C♯dim, D, Em, F♯m, G, A

As an additional check, the notes in the scale:

B, C♯, D, E, F, G♯, A

Well, uh. I used. Some of those? Would it sound better if I stuck to the 'scale-derived' chords? Know the rules before you break them and all that. Well, we can try it actually. I can map each chord in the original to the corresponding chord in B minor.

This version definitely sounds 'cleaner', but it's also... less tense I feel like. The more dissonant choices in the first one made it 'spicier'. Still, it's interesting to hear the comparison! Maybe I could reintroduce the suspended chord and some other stuff and get a bit of 'best of both worlds'? But honestly I'm pretty happy with the first version. I suppose the real question would be which one would be easier to fit a lead over...

Anyway, for the sake of argument, suppose you wanted to divide this into three melodies. One way to do it would be to slice it into low, central and high parts. These would respectively go...

Since these chords mostly move around in parallel, they all have roughly the same shape. But equally you could pick out three totally different pathways through this. You could have a part that just jumps to the nearest note it can (until the end where there wasn't an obvious place to go so I decided to dive)...

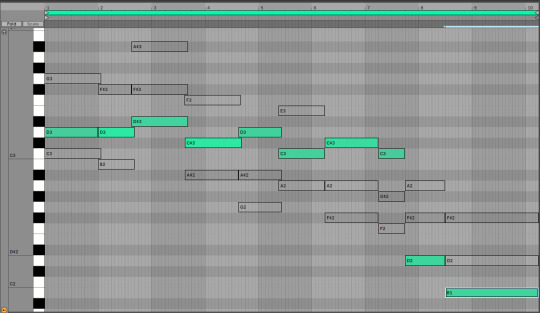
Those successive relationships between notes also exist in this track. Indeed, when two successive chords share a note, it's a whole thing (read: it gets mentioned sometimes in music theory videos). You could draw all sorts of crazy lines through the notes here if you wanted.

Nevertheless, the effects of movements between chords come in part from these relationships between successive notes. This can give the feeling of chords going 'up' or 'down', depending on which parts go up and which parts go down.

I think at this point this post is long enough that trying to get into the nitty gritty of what possible movements can exist between chords would be a bit of a step too far, and also I'm yawning a lot but I want to get the post out the door, so I let's wrap things up here. Next time: we'll continue our chord research and try and figure out how to use that Roman numeral notation. Like, taking a particular Roman numeral chord progression and see what we can build with it.

Hope this has been interesting! I'm super grateful for the warm reception the last two articles got, and while I'm getting much further from the islands of 'stuff I can speak about with confidence', fingers crossed the process of learning is also interesting...

#music theory #music notes #canmom vs music #music #composition

60 notes · View notes