#combinatorics

[knotty-et-al]

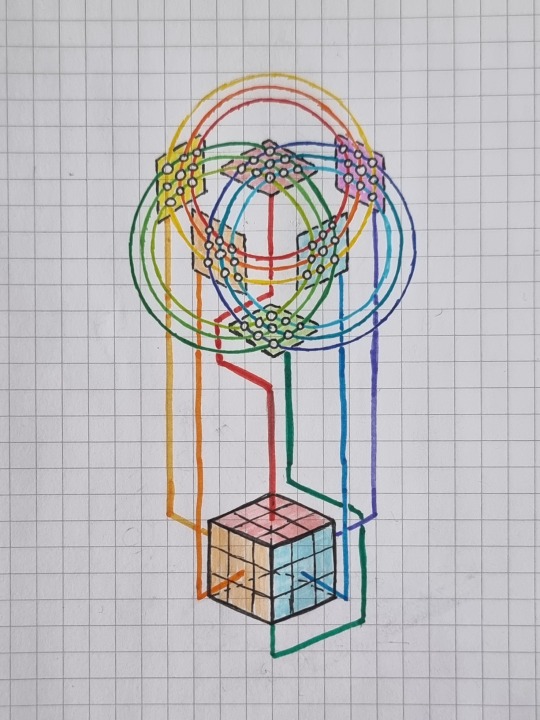
Visualization of the Rubik's cube

#permutation #permutations #groups #group theory #rubiks cube #rubikscube #math #mathematics #math visualization #visualization #knottys math #math stuff #mathy stuffy #cube #hexahedron #combinatorics

[blake447]

Combinatorics of n-Dimensional Chess

So my current project of n-dimensional chess has involved perhaps, some of the most interesting combinatorics I've ever handled. Let's talk about them! It's a perfect showcase of what I think are the 3 most important parts of math 1.> Start with simple, easy examples 2.> Break large problems into smaller parts 3.> Shift your perspective and abstract problems in a way that they are easier to deal with, while retaining a way to shift back once you've solved it to reapply what you've done. So, let's first start with the problem. Here's a piece in 5D chess known as a unicorn. It can move along any triagonal, which means it has to pick 3 out of the 5 dimensions available. in 4D time travel chess, it actually gets to move in 6 dimensional space, but it was originally introduced in space chess, a 3D variant. My point here is that n-dimensional chess means that we have to be able to list these kinds of moves for a lot of different dimensionalities, and hard coding them quite simply isnt an option. So, we turn to combinatorics!

We'll start with point 1.> by starting with our easiest example. Let's take a look at a bishop's movement in 2D space first to get a good baseline. The directions a bishop can travel along in 2D space are as follows

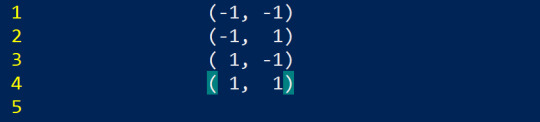
Now I purposely arranged this in a way that if we replace negative numbers with 0, we get

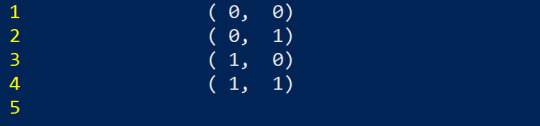
And hey! That's just counting in binary! Which makes sense, because we only have two choices, positive and negative. Once we move up to 3D space, we can actually re-use this tactic as well. Let's list all the possible combinations of directions in 3D space first, without worrying about the sign. This is what I mean in part 2.> by breaking complex problems into smaller ones, in this case breaking the movement into directions and signs.

Basically, now we can take each one of these 3 possibilities and just apply our same trick by ignoring whichever part the 0 is in. And this works for triagonals and quadragonals in higher dimensional space as well. This makes iterating through signs the easier part Of course, that means the other half is going to be the hard part. Now, with diagonals it isn't too bad. Lets look at diagonals in 5D space. Get ready because this one is a bit more of a jump

Basically what I'm doing here is I'm starting with each 1 as far left as possible, and sliding them over repeatably. not the best explanation, but its doesn't matter because this method doesn't extend well to triagonals very well (choosing 3 directions at once). Instead, we take a shift of perspective, demonstrating point 3.> Instead of representing this as a series of 1's and zeros, we simply represent the *position* of each 1. For example

We have a 1 in the 0th and 3rd locations, so we can simply represent this as just (0, 3). Suddenly, instead of trying to figure out how many ways there are to arrange 1's and 0's, we are asking how many ways can we choose 2 numbers out of 0-4. Now, there is a slight catch in that (0, 3) and (3, 0) are the same thing, so when counting them order doesn't matter, making this a simple combination problem. However we don't just want to count them, we also want to iterate over them. Lets try to generate all possible triagaonals within 7D space. That means we want to choose 3 numbers ranging from 0-6. We start with our easiest one

In order to avoid repeats (no pun intended) we maintain a strict order that is always increasing. Each number should always be larger than the previous one. To iterate through new combinations, we simply increase the last number until we can't anymore.

Now at this point, we can't increase the last number any more, so we increase the second to last and start over

And since the number after 2 has to be larger than 2, the smallest number we can roll over to is 3. From here we continue. Basically, it turns this complicated problem into a type of counting game. Just like with regular numbers, we increase the last one until it can't go anymore, then we increase the next one over and restart, just instead of restarting to 0, we restart to the smallest allowed number that keeps things in order.

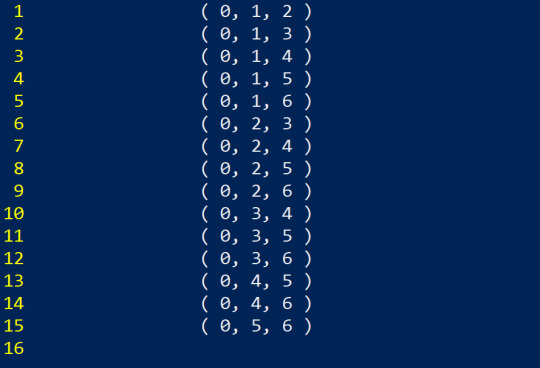
And at this point, we now have to increase our first number. I'll go ahead and finish this up despite it being pretty long, so that we can make sure we have all the possibilities

Now if we do some quick calculations for how many combinations we have of 3 numbers out of 7 total we get 3 choose 7 = 7! / ( 3! * (7-3)! ) = 7! / ( 3! * 4! ) = (7 * 6 * 5) / (3 * 2 * 1) = (7 * 5) = 35

Which is exactly how much we counted to! There are a few reasons we know there aren't any repeats but this has gotten long enough, and I can't quite articulate them off the top of my head. From here we convert back into 1's and 0's, then we count up in binary for each one of them to get the sign permutations. To wrap things up, I'll finish up by demonstrating all those sign permutations for one of these direction combinations. As stated in point 3.> we can translate back from our abstraction back to the original problem, so we can apply the smaller part that is generating the sign permutations.

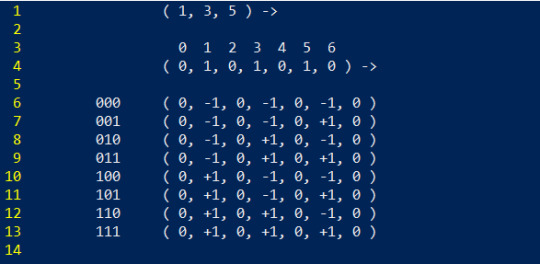
There we go. A little bit of a mess, but that's it! And that's how I generate arbitrary m-agonals in arbitrary n-dimensional space for my chess engine. Finally, here's a picture of a queen's movement allowed to move along any agonal up to heptagonals (seven!) on a 7D board generated in a precursor to my current iteration of nDimensional chess

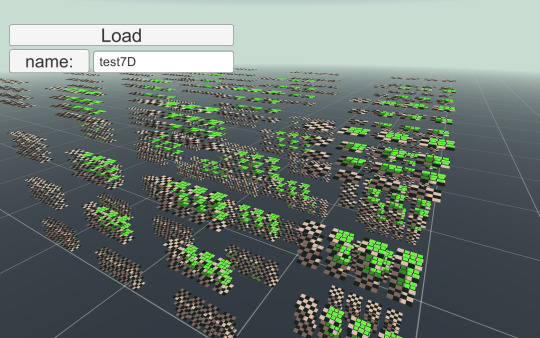
Y'know, not that anyone would ever play that lol. Here's a bishop on the same board, which is (somewhat) more... manageable lol.

And that's all I got! this math right here is the bread and butter of what makes n-dimensional chess possible! and is potentially one of my favorite problems I've worked on.

#mathblr #math #programming #combinatorics #chess #chessboard #5D Chess #gamedev #progblr #codeblr #coding #mathematics

[cecilias-cool-stuff]

Today in "Wow, people in the 60s were really Like That":

#math #combinatorics #this is the paper that defines parking functions

[cant-think-of-a-good-one]

TFW - that feeling when

FTW - for the win

WTF - what the fuck

TWF - ?

FWT - ?

WFT - ?

#words #combinatorics

[futurebird]

What if the Library of Babel contained books, not just texts.

I love the Library of Babel-- but it's important to remember that it contains all *texts* (up to a certain length) this is not the same as containing all *books* -- books are objects, they can be different shapes and sizes, made of different materials, bound with different bindings-- books have highlighting and margin notes from previous readers, old lending cards with the names of readers and dates.

Books can have illustrations. But we could make a Babel style indexing system for possible print images. Then represent the images as their index number. Now we have illustrations. We could have codes for size, color, cover material, paper weight, illustrations, margin notes, the style of handwriting of the margin notes. It would be a complex system and the final index numbers would need to be much longer. Possibly impractically long. But, a finite thing can be impractically large.

Here is a related question. How many distinct (as in you can distinguish between them yourself) objects can fit in a breadbox?

(Not all at once. I'm asking how many "different" things are small enough to be placed in a breadbox. This is either permutations or philosophy. )

#library of babel #babel #books #mathematics #combinatorics #permutations #infinity #aleph #aleph null #continuum #continuum hypothesis #math question #library #very large numbers

[art-of-mathematics]

June Huh wasn’t interested in mathematics until a chance encounter during his sixth year of college. Now his profound insights connecting combinatorics and geometry have led to math’s highest honor.

June Huh often finds himself lost. Every afternoon, he takes a long walk around Princeton University, where he’s a professor in the mathematics department. On this particular day in mid-May, he’s making his way through the woods around the nearby Institute for Advanced Study — “Just so you know,” he says as he considers a fork in the path ahead, “I don’t know where we are” — pausing every so often to point out the subtle movements of wildlife hiding beneath leaves or behind trees. Among the animals he spots over the next two hours of wandering are a pair of frogs, a red-crested bird, a turtle the size of a thimble, and a quick-footed fox, each given its own quiet moment of observation.

“I’m very good at finding stuff,” he says. “That’s one of my special abilities.”

Huh, 39, has now been awarded the Fields Medal, the highest honor in mathematics, for his ability to wander through mathematical landscapes and find just the right objects — objects that he then uses to get the seemingly disparate fields of geometry and combinatorics to talk to each other in new and exciting ways. Starting in graduate school, he has solved several major problems in combinatorics, forging a circuitous route by way of other branches of math to get to the heart of each proof. Every time, finding that path is akin to a “little miracle,” Huh said.

One might say the same of his path into mathematics itself: that it was characterized by much wandering and a series of small miracles. When he was younger, Huh had no desire to be a mathematician. He was indifferent to the subject, and he dropped out of high school to become a poet. It would take a chance encounter during his university years — and many moments of feeling lost — for him to find that mathematics held what he’d been looking for all along.

After reading the article - he gives off much of the Ramanujan and overall unconventional and enthusiastic neurodivergent vibes. And it makes me happy to read.

#math #math and art #mathematician #interesting twists #poetry #poetry and math #creative ways to see the world #combinatorics #geometry #mathematics #a new way to see #quanta magazine #june huh #fields medal #inspiring #enthusiasm #curiosity

[storymaker14]

Permutohedron, Associahedron, and Cyclohedron

"But does he do things other than write?" I'm glad you asked!

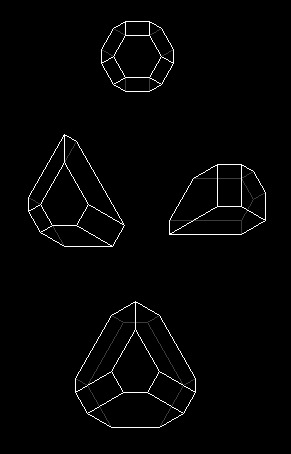
Behold: the permutohedron, the associahedron, and the cyclohedron, in three spatial dimensions.

Why did I specify three spatial dimensions? Because I'm working on drawing the three dimensional cross-sections of the four-dimensional versions of them. Why? Why not!

I've already got the slices of the 4-permutohedron done, because seriously, they're a piece of piss. Working on the 4-associahedron, slowly but surely. The 4-cyclohedron... may take some time, because it's a doozy of a shape.

Watch this space.

***

Okay, so, the slices of the four-dimensional permutohedron look like:

As for the 4-associahedron, there are eight (I think) different ways to slice it, so I went with by far the one that takes the least time and effort:

I've only just started plotting the vertexes, edges, and faces of the 4-cyclohedron; good news, only one set of slices, but bad news, they're huge and very time intensive to fully plot. So, I cannot make guarantees when or even if I'll get them posted, but it'll be a while at least.

***

Like I said, a while. However:

That was fun. What now?

#beauty in math #math #geometry #monochrome #combinatorics

[truonghoc]

how many ways can you choose 8 out of 26 letters of the english alphabet?!!!

why do passwords require you to use 8 characters? and what happens if you restrict these characters to only letters and no symbols...

there are 26 letters of the english alphabet. so there are 26 different ways to choose a single letter... we are simple for now.

DISCLAIMER: i specify english alphabet because i know for sure it has 26 letters! other languages (even those using the latin alphabet) can have different numbers of letters.

and then we want to pick a second letter... there are 26 different ways to choose another letter. fantastic! this is the same as before.

how many ways are there to pick a combination of two letters? hmmm... if there are 26 ways to pick the first letter and 26 ways to pick the second letter... well i'm stumped. i don't know if i should add these 26 + 26 or multiply these 26 x 26 or divide these 26 / 26 or what???! or maybe 26^26... this is too much to think about.

i will detour to the concept of "probability" which is intrinsically linked to the idea of "how many ways can (x) happen"

probability detour

what is the probability of choosing one specific letter - let's say "A" - from the alphabet? well...

"A" is just one letter from the alphabet, so we know there's only one "A"... or only "one way to choose A"

choose A for what? it doesn't matter! choose A for eating, choose A to put in the left side of a box... whatever works for your situation.

in any case, there is only 1 A, but there are 26 letters in the alphabet that you could potentially choose. you could say "there is only one out of twenty-six ways i could choose A!!!"...

and one way of expressing "(A) out of a total (B)" is as a fraction, A/B. we call this a "probability", which relates to our chances of something happening. so our probability of choosing A out of a box of 26 letters is 1/26, or a more familiar 3.8% chance.

we can understand probability better with a classic (maybe beaten-to-the-ground) example of a coin toss. let's make up a game with the following rules:

every single person on earth has to toss a coin

every person whose coin lands on the "heads" side can keep playing

every person whose coin lands on "tails" will stop playing

ROUND 1: since there's a 1/2 chance of landing heads, only about half of the people on earth can keep playing.

ROUND 2: half of the half remaining players keep playing... this is 1/4 of the original player population

ROUND 3: half of the half of the half of the remaining players keep playing... this is 1/8 of the original player population

it just keeps cutting in half!!! what?!!!

we can think of each consecutive round as "halving" the number of players. we can write this mathematically as continuously dividing by 2

original # of players in round 1, a number that i like to call "P" for "players"

-> P/2 players in round 2

-> (P/2)/2 = P/4 players in round 3

-> ((P/2)/2)/2 = (P/4)/2 = P/8 players in round 4

and so on....

we can express this as multiplying by (1/2) also! this is because dividing by a number is the same as multiplying by 1/(that number).

so it's like for the third round it's like (1/2)(1/2)(1/2), and for the fourth it's like (1/2)(1/2)(1/2)(1/2)... and it gets tiring to write out this multiplication. what if we play 100 rounds? i don't want to write that out 100 times! we'll write it using this little hat: ^

so writing (1/2)^100 means we've multiplied 1/2 together 100 times. from our previous example, we know that with a certain number ("n" for number) of rounds, the population of players will have been cut in half n times or multiplied by (1/2)^n.

and remembering that the denominator (the number in the "basement" of the fraction) in a probability represents the total number of potential options... then there are 2^n potential results for n coin flips!

for example, 2 coin flips could result in:

heads then tails

tails then heads

heads then heads

tails then tails

we could get this number "4" from the expression 2^2, where the first 2 represents the number of possible outcomes and the second 2 comes from the number of trials.

when we apply this to the alphabet...

let's think of our "entire world population" again.

1/26 of people will choose the letter "A".

then 1/26 of those 1/26 people will choose the letter "A".

then 1/26 of the 1/26 of the 1/26 will choose "A". do you see where i'm going with this?

if there are 8 "trials", we'll get (1/26)^8 people choosing "A", which is like a 0.00000000048% chance of choosing "A".

this means there are 26^8 = 208827064576 ways to choose 8 letters out of the alphabet!!! SO MANY!!!

so 8-letter passwords give a lot of possibility, even if you're just restricted to letters. it's hard to hack into a system with 208827064576 possibilities of passwords!

but this is only if you can reuse letters... what if you can't reuse letters?

will the number of possible passwords reduce? and how will we express this reduction? the answer is... factorials! which i may or may not discuss.

#probability #combinatorics

[euler-of-a-leonhard]

2022-11-24: Permutahedron of order 3

#math #combinatorics

[blake447]

So here's an interesting fact I've learned while researching these things called Wolstenholme Primes. See they're related to the binomial coefficient and thus pascals triangle. We've probably all seen sierpinski's triangle in here (if not circle all the odd numbers). But here's something else interesting. If you look at the triangle, you'll see that for prime numbers, every element is divisible by that prime number. Look at 11 for example.

55, 165, 330, and 462 are all divisible by 11. This has to do with the binomial coefficient definition, in which you'll see that if unless we choose either all the elements, or none of them, the factor of our prime number is guaranteed not to cancel out from the numerator's factorial.

We can then use the fact that the sum of all the elements in the nth row of pascal's triangle adds up to 2^n. Once we remove the 1's on each end of the triangle (hence the minus 2) we know that for prime numbers p that all elements are divisible by p, their sum is as well!

Now, I don't know off the top my head if this is only true for prime numbers. It isn't immediately obvious imo. However, if this is strong enough to be an if and only if, then I think I have independently discovered perhaps the *worst* way to test for primality lmao, scaling exponentially instead of the standard logarithmically.

#mathematics #math #pascals triangle #combinatorics #binomial #binomial coefficient #prime numbers #number theory #mathblr

[cecilias-cool-stuff]

New puzzle, that involves some graph theory!

An "n-cycle" is a graph that looks like a polygon with n vertices. An "independent set" of a graph is a subset of the vertices of the graph such that no pair of vertices in the subset are connected by an edge. How many k-element independent sets of an n-cycle exist?

#math #puzzles #graph theory #combinatorics #mathematics

[drberfarious]

combinatorics out of context:

"case 6: nothing is equal"

#mathematics #mathblr #math #combinatorics

[anonymouscapybara]

the pigeonhole principle states that if you put a pigeon in a hole, then seal off the hole so that no air can get through, then the pigeon will suffocate and die. this may seem obvious, but it has some highly nontrivial applications. try using it to prove that P≠NP! (pigeon≠no-pigeon)

#math #combinatorics

[futurebird]

Why the Library of Babel feels impossible... but isn't.

I think I see through the magic trick of the The Library of Babel a little better now. Not that anything about it is "fake" --just that part of what makes it feel impossible is going to a room and finding a book on a particular shelf feels like a very finite act-- but "every book possible" feels infinite.

Feels.

The hexagons have very long names. It's critical that the books use only lower case letters, otherwise the names would be laughably long. The hexagon names are a more dense encoding because they use a larger character set. (they use A-Z, a-z, 0-9, not just lowercase letters) So they form a correspondence with a much larger set than you might expect. I stumbled into this while thinking about looking up the names of books in books. And that causes something of a 'small' problem! You don't have the characters required to write book names into books, you'd need to write out the numbers as words, or find some other way to express that big chunk of text above through encoding. It will take up too much space. Books can't contain book titles and locations.

#math #one to one correspondence #data denisty #combinatorics #permulations #library of babel #library

[art-of-mathematics]

Some new illustrations/word art for my project "Iteration book"...

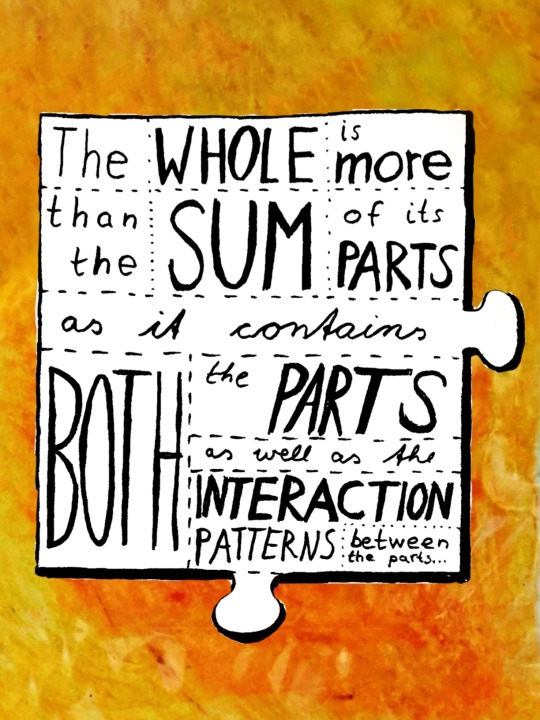
"The whole is more than the sum of its parts, as it contains both the parts as well as the interaction patterns between the parts."

"1. Life is like a jigsaw puzzle…

2. Every puzzle piece is an entire jigsaw puzzle on its own…

3.1. Each iteration of puzzling alters the big picture slightly…

3.2. and renders the big picture with additional details... "

3.3. and corrects errors along the way of rendering the big picture."

#i might write the img captions later #iteration book #iteration #math art #math #my art #art #quotes #quote #the whole is more than the sum of its parts #math quote #my quotes #concept art #recursive puzzle #jigsaw puzzle #combinatorics #dynamical systems #patterns #dancing patterns #analogies #analogy #chaos theory #chaos #fractal geometry #fractal #fractals #STEM art #jigsaw

[iuiw]

2558749 25 55 58 27 34 49 25 27 34 49 55 58 3804824 38 20 04 48 22 24 04 20 22 24 38 48 095695601 09 35 56 39 35 56 60 01 01 09 35 39 56 60 4405480 44 40 05 54 48 20 05 20 40 44 48 54 2698134 26 09 38 21 13 34 09 13 21 26 34 38 7258186 12 25 58 21 18 26 12 18 21 25 26 58 1208184 12 20 08 21 18 24 08 12 18 20 21 24 7102132 11 10 02 21 13 32 02 10 11 13 21 32 8412869 24 31 12 28 26 09 09 12 24 26 28 31 8513289 25 51 13 32 28 29 13 25 28 29 32 51 33560609 33 35 56 60 06 60 09 06 09 33 35 56 60 9122844 31 12 22 28 24 44 12 22 24 28 31 44 9635462 36 03 35 54 46 02 02 03 35 36 46 54

#math #megassena #combinatorics